Blog
Reinforcement Learning Concepts

Reinforcement Learning Concepts

April 25, 2025·Deependu
Deependu

What is Reinforcement Learning?

rl

  • Learning from interaction with the environment.
  • Agent observes the environment and takes actions on it.
  • The environment provides feedback in the form of rewards.
<p>The agent learns to maximize the cumulative reward over time.</p>

Episodic vs Continuing Tasks

  • Episodic Tasks: The task has a clear beginning and end. tic-tac-toe is an example of an episodic task.
  • Continuing Tasks: The task does not have a clear end. stock trading is an example of a continuing task.

Discount factor

  • If the agent’s aim is to maximize the cumulative reward, for continuing tasks, the total reward can be infinite.
  • To avoid this, we use a discount factor γ (gamma) to reduce the value of future rewards.
  • The discount factor is a number between 0 and 1.
  • This bounds the total reward to a finite value.

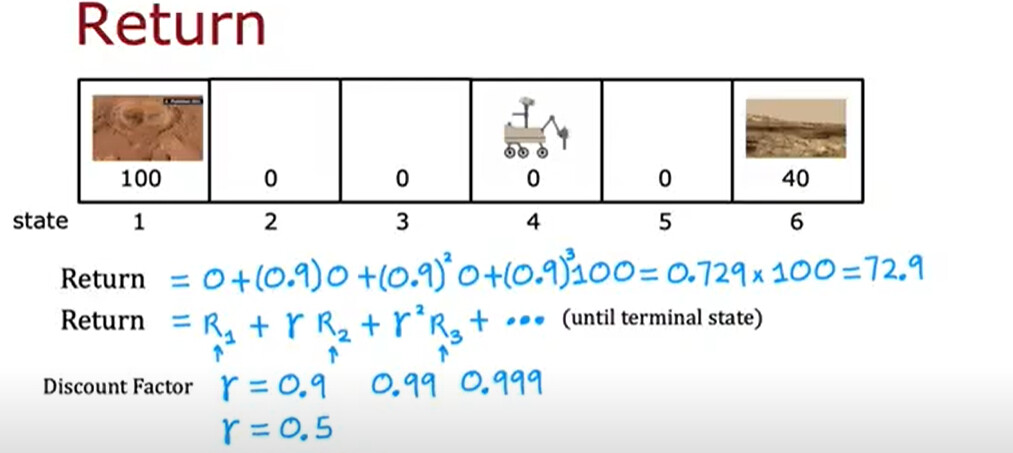
Discount factor

<ul> <li>Higher gamma means the agent will consider future rewards more.</li> <li>Lower gamma means the agent will consider immediate rewards more.</li> <li>The discount factor is a hyperparameter that can be tuned based on the task.</li> </ul>

Terminology

  • Agent: The learner or decision maker.
  • Environment: The external system that the agent interacts with.
  • State: A representation of the environment at a given time.
  • Observation: The information the agent receives from the environment.
  • Action: The set of all possible actions the agent can take.
  • Policy: A strategy that the agent employs to determine the next action based on the current state.
  • Reward: A scalar feedback signal received from the environment after taking an action.
<p>Remember: Observation won&rsquo;t always be equal to state. For example, a robot may only see what&rsquo;s in front of it, but the state may include the entire environment.</p>

Value Functions

A function that estimates the expected return (cumulative reward) from a given state or action.

State-Value Function (V)

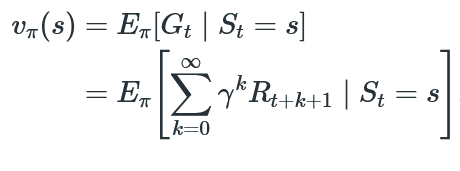
State-Value Function

  • The expected return from a state s under a policy $\pi$.
  • It’s like, if I reach state s, and then I follow the policy $\pi$, what’s the maximum reward I can get?

Action-Value Function (Q)

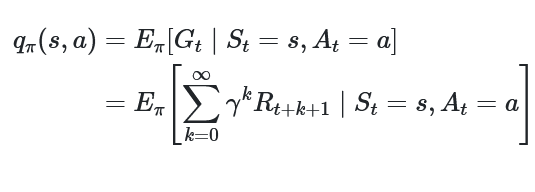
Action-Value Function

  • The expected return from a state s and action a under a policy $\pi$.
  • Think of it like, if I reach state s and there I take action a, and after that I follow the policy $\pi$, what’s the maximum reward I can get?
But what exactly is state-value & action-value function?

First, let’s understand: What is policy?

  • A policy is like strict parents, they tell you what to do in which situation.
  • If it’s 9 PM, don’t use your phone, If it’s 10 PM, go to bed.
  • So, a policy is a mapping from state to action.
  • A policy can be deterministic or stochastic.
  • A deterministic policy is like: when in state s, do action a.
  • A stochastic policy is like: when in state s, do action a with probability p, and action b with probability q. (p + q <= 1)

Now, let’s understand: What is state-value function?

  • The state-value function is like: your newbie trader friend telling you, if you somehow just start trading, you will make $100000 in 1 month.
  • So, it’s like, if you reach state s, and follow the policy $\pi$ (his instagram course-seller guru), you will get $1000 in 1 month.
  • It says nothing about the action you take, just the state you are in.
<p>So, it&rsquo;s like a mapping from state to expected return.</p>

Now: What is action-value function?

  • Now, your friend tells you, if you start trading and buy AAPL stock, and after that you follow his instagram course-seller guru, you will make $100000 in 1 month.
  • So, it’s like, if you reach state s, and take action a, and after that you follow the policy $\pi$ (his instagram course-seller guru), you will make $100000 in 1 month.
<ul> <li>Here, We also consider the action that you need to take after reaching the state.</li> <li>So, it&rsquo;s like a mapping from state-action pair to expected return.</li> </ul>
<ul> <li>If you reach stanford, you can become a millionaire. (state-value function)</li> <li>If you reach stanford and do a cs degree, you can become a millionaire. (action-value function)</li> </ul>

Markov Decision Process (MDP)

  • If I’ve complete details of the current state, I can predict the just next state. I don’t need to know the previous states.
<ul> <li>Anything that satisfies the Markov property is called a Markov process.</li> <li>And, we can we make something satisfy the Markov property by adding some extra information to the state.</li> </ul>

Bellman Equation

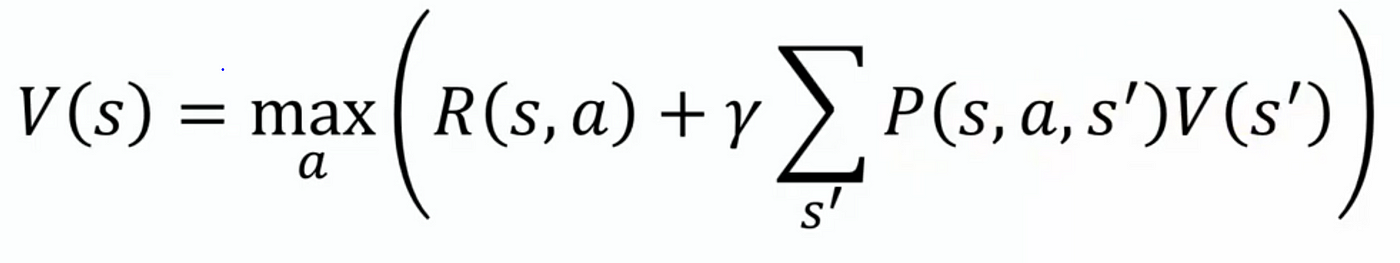
state-value bellman equation

<p>max value of the immediate reward for all possible actions + value of the next state.</p>

action-value bellman equation

<p>expected value of the immediate reward + expected value of the next state.</p>

What’s Next?

Enough concepts, now let’s play with Q-Learning and Deep Q-Learning.

Check out the Q-Learning and Deep Q-Learning blogs to learn more about these algorithms.

Last updated on
Q-Learning