Blog
Q-Learning

Q-Learning

April 25, 2025·Deependu
Deependu

Q-learning is a model-free reinforcement learning algorithm used to train agents (computer programs) to make optimal decisions by interacting with an environment.

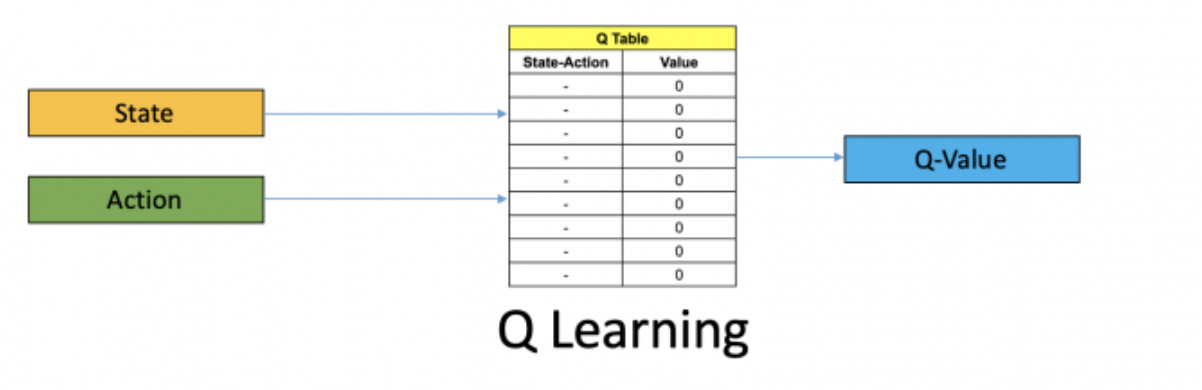
q-learning

What is Q-Value?

  • Q-value (or action-value) is a mapping from state-action pairs to expected future rewards.
  • The Q-value is denoted as Q(s, a).

$$ Q(s, a) = E[R_t | s_t = s, a_t = a] $$

expected future reward if the agent is in state `s` and takes action `a`.

Bellman Equation

  • The Bellman equation is a recursive equation that relates the value of a state to the values of its successor states.

$$ Q(s, a) = r + \gamma \max_{a’} Q(s’, a’) $$

  • Where:
    • r is the immediate reward received after taking action a in state s.
    • γ (gamma) is the discount factor, which determines the importance of future rewards.
    • s' is the next state after taking action a in state s.
    • a' is the next action taken in state s'.
  • The Bellman equation is used to update the Q-value for a given state-action pair.

Temporal Difference Learning

  • Temporal difference (TD) learning means, we don’t wait for the final outcome to update the Q-value.
  • Instead, we update the Q-value based on the immediate reward and the estimated value of the next state.
It's like:

- You drive 10 meters — it feels good, so you think: "Hey, driving is fun!" (reward!)
- You drive 100 meters and reach KFC — it feels even better!

Now — when you first started, you didn’t know driving 10 meters was leading to the KFC.

Over time, you realize:

- "Ohh, that small 10-meter drive was actually important, because it eventually got me to the KFC!"

Temporal Difference Update Rule

  • In Q-learning, we use the TD update rule to update the Q-value for a given state-action pair.
  • We’d some initial estimate for the Q-value in some state s and action a. When we actually take action a in state s, we get a reward r and move to the next state s' with some max Q-value for some possible action a'.
  • So, we would like to update the Q-value for the state-action pair (s, a), but we don’t want to completely forget the previous estimate. Who knows, maybe it was a good estimate.
  • So, we use a learning rate α (alpha) to control how much we want to update the Q-value.

$$ Q(s, a) \leftarrow Q_{old}(s,a) + \alpha [Q_{new}(s,a) - Q_{old}(s,a)] $$

$$ Q(s, a) \leftarrow Q(s, a) + \alpha [r + \gamma \max_{a’} Q(s’, a’) - Q(s, a)] $$

Epsilon-Greedy Policy

  • Choose the best action with probability 1 - ε (epsilon).
  • Choose a random action with probability ε.
  • This helps the agent to explore new actions and avoid getting stuck in local optima.
Introduce randomness in the action selection process to explore the environment.

Q-Learning approach

Q-Learning Approach

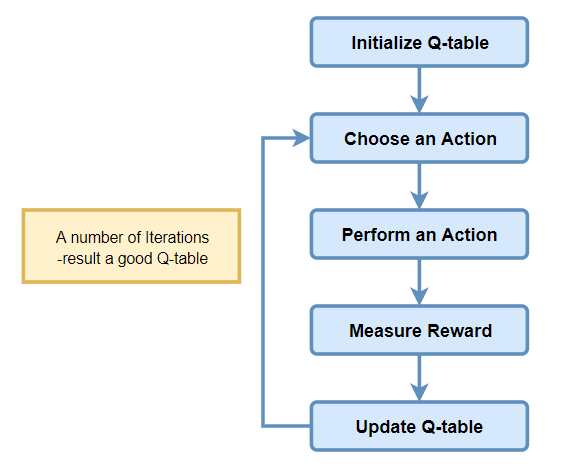
Python Implementation 

import numpy as np
import matplotlib.pyplot as plt

# Parameters
n_states = 16  
n_actions = 4 
goal_state = 15 

Q_table = np.zeros((n_states, n_actions))

learning_rate = 0.8
discount_factor = 0.95
exploration_prob = 0.2
epochs = 1000

# Q-learning process
for epoch in range(epochs):
    current_state = np.random.randint(0, n_states) 

    while current_state != goal_state:
        
        # Exploration vs. Exploitation (ϵ-greedy policy)
        if np.random.rand() < exploration_prob:
            action = np.random.randint(0, n_actions)  
        else:
            action = np.argmax(Q_table[current_state]) 

        # Transition to the next state (circular movement for simplicity)
        next_state = (current_state + 1) % n_states

        # Reward function (1 if goal_state reached, 0 otherwise)
        reward = 1 if next_state == goal_state else 0

        # Q-value update rule (TD update)
        Q_table[current_state, action] += learning_rate * \
            (reward + discount_factor * np.max(Q_table[next_state]) - Q_table[current_state, action])

        current_state = next_state  # Update current state

# Visualization of the Q-table in a grid format 
q_values_grid = np.max(Q_table, axis=1).reshape((4, 4)) 

# Plot the grid of Q-values
plt.figure(figsize=(6, 6))
plt.imshow(q_values_grid, cmap='coolwarm', interpolation='nearest')
plt.colorbar(label='Q-value')
plt.title('Learned Q-values for each state')
plt.xticks(np.arange(4), ['0', '1', '2', '3'])
plt.yticks(np.arange(4), ['0', '1', '2', '3'])
plt.gca().invert_yaxis()  # To match grid layout
plt.grid(True)

# Annotating the Q-values on the grid
for i in range(4):
    for j in range(4):
        plt.text(j, i, f'{q_values_grid[i, j]:.2f}', ha='center', va='center', color='black')

plt.show()

# Print learned Q-table
print("Learned Q-table:")
print(Q_table)
Last updated on
Reinforcement Learning ConceptsDeep Q-Learning (DQN)